1. 기수 정렬 개념
기수 정렬은 지금까지 살펴보았던 비교 기반 정렬 알고리즘이 아닌 분배 기반 정렬 알고리즘입니다.
미리 데이터를 담을 공간을 마련해두고, 기준에 따라 데이터를 담았다 꺼내는 방식으로 정렬합니다.
우리가 흔히 엑셀에서 서로 다른 기준으로 정렬할 때 사용하는 방식과 비슷하게 진행됩니다.
예를 들어 다음 그림과 같은 다섯 명의 사람이 있을 때, 남자를 앞에 여자를 뒤에(성별 기준), 그리고 가나다 순(이름 기준)으로 정렬하려면 어떻게 해야할까요?
정답은 최우선 기준을 마지막에, 차선 기준을 먼저 정렬해야합니다.
따라서 먼저 가나다 순(이름 기준)으로 정렬합니다.
다음으로 상대적인 위치를 바꾸지 않으면서 남자와 여자로 정렬합니다.
결과적으로 성별 기준을 우선으로, 그다음 이름(가나다 순)으로 정렬되었습니다.
정수를 정렬할 때도 마찬가지입니다.
초등학교 수학 시간에 배우듯 수의 크기 비교는 더 큰 자릿수가 우선입니다.
따라서 기수 정렬을 할 때에는 작은 자릿수부터 기준으로 정렬합니다.
2. 기수 정렬 예제
다음 수를 기수 정렬 해봅시다.
가장 큰 수가 세 자리 수이므로, 일의 자리부터 백의 자리까지 총 세 번 반복합니다.
먼저, 숫자들을 하나씩 살펴보며 일의 자리 숫자에 따라 나누어 담습니다.
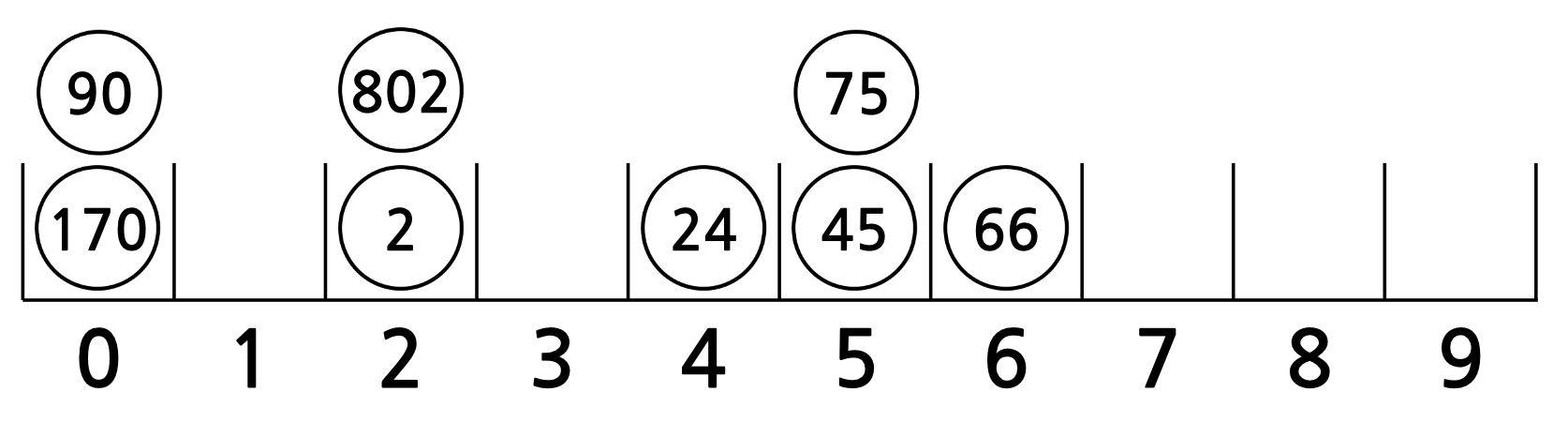
다시 꺼냅니다.
이때 데이터를 담는 자료구조가 큐(선입선출)라면 앞에서부터 꺼냅니다.
만약 스택(후입선출)이라면 뒤에서 꺼내면 됩니다.
일의 자리를 기준으로 숫자가 정렬되었습니다.
이번엔 십의 자리 숫자에 따라 순서대로 담습니다.
다시 꺼냅니다.
이제 두 자리 수 기준으로는 정렬이 되어 있습니다.
또 중요한 점이, 2와 802를 보면 두 수 모두 두 자리 수 기준으로 같은 값을 가지지만 상대적인 위치가 변하지 않습니다.(안정적인 정렬)
마지막으로 백의 자리 숫자에 따라 순서대로 담습니다.
다시 꺼내면 정렬이 완료됩니다.
3. 기수 정렬 코드
nums = [170, 45, 75, 90, 2, 24, 802, 66]
def radix_sort(nums):
# 주어진 수의 최대 자릿수가 얼마인지 확인
max_num = max(nums)
d = 0
while max_num // (10**d):
d += 1
# 최대 자릿수 만큼 반복
for i in range(d):
# 각 자릿수에 따라 나누어 담을 공간
buckets = [[] for _ in range(10)]
# 각 자릿수에 따라 나누어 담음
for num in nums:
buckets[(num//(10**i))%10].append(num)
# 담았던 숫자들을 차례대로 하나씩 꺼내어 nums를 갱신
j = 0
for bucket in buckets:
for num in bucket:
nums[j] = num
j += 1
radix_sort(nums)
print(nums)
# [2, 24, 45, 66, 75, 90, 170, 802]4. 기수 정렬 장점
기수 정렬은 시간 복잡도가 \(O(n)\)으로 매우 효율적입니다.
안정적인 정렬로 같은 값을 가지는 원소의 상대 위치가 바뀌지 않습니다.
5. 기수 정렬 단점
데이터의 자릿수가 많아지면 효율성이 떨어질 수 있습니다.
정수나 정수로 표현할 수 없는 데이터는 정렬할 수 없습니다.
제자리 정렬이 아니고 추가적인 공간이 필요합니다.
6. 정렬 알고리즘 시간 복잡도 비교
| 정렬 알고리즘 | 최악(Worst) | 최선(Best) | 평균(Average) |
| 버블 정렬(Bubble Sort) | \(O(n^2)\) | \(O(n^2)\) | \(O(n^2)\) |
| 선택 정렬(Selection Sort) | \(O(n^2)\) | \(O(n^2)\) | \(O(n^2)\) |
| 삽입 정렬(Insertion Sort) | \(O(n^2)\) | \(O(n)\) | \(O(n^2)\) |
| 퀵 정렬(Quick Sort) | \(O(n^2)\) | \(O(n\log{n})\) | \(O(n\log{n})\) |
| 병합 정렬(Merge Sort) | \(O(n\log{n})\) | \(O(n\log{n})\) | \(O(n\log{n})\) |
| 힙 정렬(Heap Sort) | \(O(n\log{n})\) | \(O(n\log{n})\) | \(O(n\log{n})\) |
| 기수 정렬(Radix Sort) | \(\boldsymbol{O(n)}\) | \(\boldsymbol{O(n)}\) | \(\boldsymbol{O(n)}\) |
| 계수 정렬(Counting Sort) | \(O(n)\) | \(O(n)\) | \(O(n)\) |
