
1. 강한 연결 요소(SCC; Strongly Connected Components)
유향 그래프(Directed Graph)에서 모든 정점이 다른 모든 정점에 도달할 수 있는 경우, 강하게 연결되었다고 합니다.
다시 말하면, 임의의 두 정점 사이에 한 정점에서 다른 정점으로, 그리고 다시 다른 정점에서 원래 정점으로 경로(사이클)가 존재하는 것을 의미합니다.
무향 그래프의 경우에는 정점이 연결만 되어 있다면 다른 연결된 모든 정점에 도달할 수 있기 때문에 의미가 없습니다.
유향 그래프에서 강하게 연결된 최대 부분 그래프를 강한 연결 요소라고 합니다.
강한 연결 요소를 하나의 정점으로 만드는 것을 응축이라고 하고, 그렇게 만들어진 유향 그래프는 유향 비순환 그래프(DAG; Directed Acyclic Graph)가 되고, 위상 정렬이 가능해집니다.

https://ko.wikipedia.org/wiki/강한_연결_요소
강한 연결 요소 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 그래프에 강한 연결 요소를 표시한 모습 유향 그래프에서 모든 정점이 모든 다른 정점에 대해 도달 가능한 경우, 그래프는 강하게 연결되었다 또는 상호연결
ko.wikipedia.org
2. 타잔의 SCC 알고리즘
이 알고리즘의 기본 동작은 깊이 우선 탐색(DFS; Depth First Search)입니다.
깊이 우선 탐색에 더하여 추가적인 연산을 수행합니다.
먼저, 탐색 순서를 id로 하여 정점을 구분합니다.
낮은 숫자(lowlink) 값을 관리하며 강하게 연결되었는지 확인합니다.
그리고 탐색 정점을 담아 관리할 stack을 사용합니다.
깊이 우선 탐색과 별개로 SCC 확인이 끝났는지 확인할 finished를 따로 관리합니다.

1.

탐색의 첫 번째 정점은 id가 1, 이고 low 값은 본인의 id인 1입니다.
스택에 해당 정점을 담습니다.
stack = [1]
2.

깊이 우선 탐색에 따라 두 번째 정점을 탐색하고, 탐색된 적이 없기 때문에 id는 2, low 값는 2가 됩니다.
stack = [1, 2]
3.

2와 마찬가지 과정이 반복됩니다.
stack = [1, 2, 3]
4.

다음 정점(1번 정점)이 이미 탐색이 완료된 정점이지만, SCC를 확인하지는 않았습니다.
따라서 1을 받아 3번 정점의 lowlink 값이 더 작은 값인 1이 됩니다.
stack = [1, 2, 3]
5.

재귀적으로 다시 2번 정점으로 거슬러 올라가 이전에 사용한 lowlink 1이 반환됩니다.
원래 lowlink 값보다 1이 작으므로 2번 정점의 lowlink 값이 1이 됩니다.
stack = [1, 2, 3]
6.
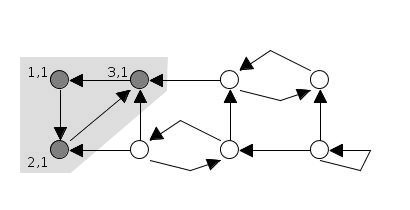
한 번 더 재귀적으로 거슬러 올라가면 1번 정점에 도착하고, lowlink 값이 id 값과 같습니다.
그렇다는 것은 사이클(강한 연결)이 확인된 것이고, stack에서 해당 정점이 나올 때까지 꺼냅니다.
꺼내면서 정점들은 SCC가 확인됐으므로 finished에 등록하고, 그렇게 꺼내어진 [3, 2, 1]은 SCC가 됩니다.
stack = []
SCC = [[3, 2, 1]]
7.
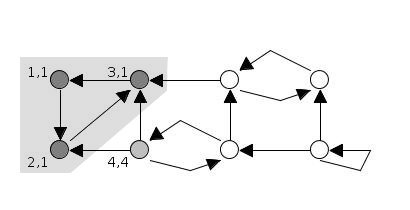
2, 3번 정점은 탐색과 SCC 확인이 끝났으므로, 4번 정점에서 DFS를 시작합니다.
stack = [4]
SCC = [[3, 2, 1]]
8.
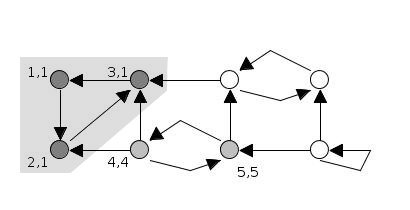
DFS를 계속 진행합니다.
stack = [4, 5]
SCC = [[3, 2, 1]]
9.

stack = [4, 5, 6]
SCC = [[3, 2, 1]]
10.
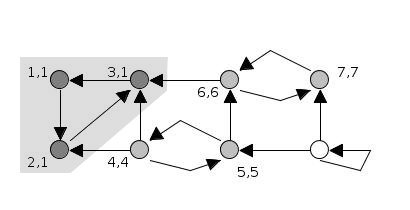
stack = [4, 5, 6, 7]
SCC = [[3, 2, 1]]
11.
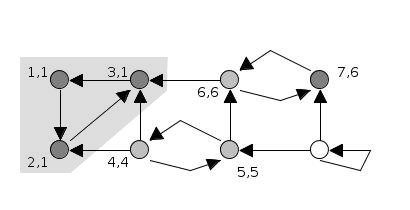
6번 정점은 탐색이 끝났고, low 값이 6이므로 7번 정점의 low 값이 6이 됩니다.
stack = [4, 5, 6, 7]
SCC = [[3, 2, 1]]
12.
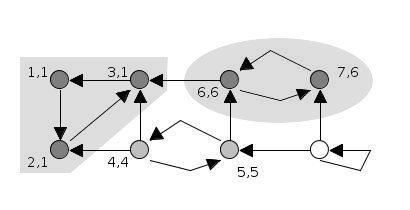
7번 정점에서 더 이상 탐색이 안되므로, 7번 정점의 low 값인 6을 반환합니다.
반환된 6을 받은 6번 정점은 자신의 low 값이 6이 되고, 자신의 id와 같으므로 stack에서 자신이 나올 때까지 pop 합니다.
pop 하면서 SCC 확인이 완료된 정점들은 finished에 등록합니다.
stack = [4, 5]
SCC = [[3, 2, 1], [7, 6]]
13.
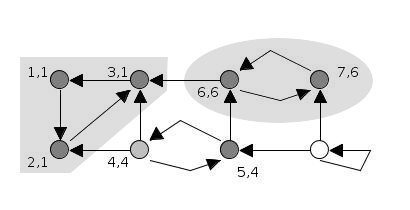
6번 정점의 탐색이 끝나 6을 반환하고, 6을 반환받은 5번 정점은 기존 low 값인 5가 더 작으므로 id는 5입니다.
5번 정점에서 다음 탐색 대상인 4번 정점으로 탐색을 이어나가면, 4번 정점은 탐색을 완료했으므로 4를 반환하고, 5번 정점의 low 값은 4가 됩니다.
stack = [4, 5]
SCC = [[3, 2, 1], [7, 6]]
14.
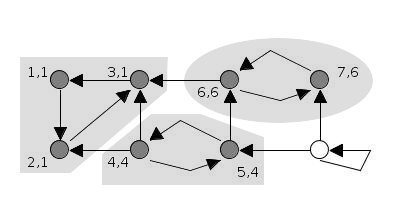
5번 정점에서의 탐색이 끝나 low 값 4를 반환하고, 이것을 반환 받은 4번 정점은 low 값이 4가 되어 자신의 id와 같습니다.
사이클이 확인되었으므로 stack에서 자신이 나올 때까지 pop 하며 finished와 SCC에 추가합니다.
stack = []
SCC = [[3, 2, 1], [7, 6], [5, 4]]
15.
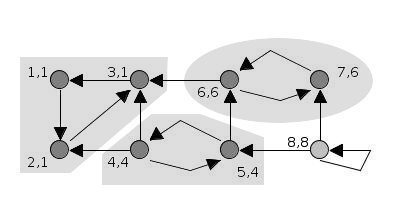
DFS를 이어나가면 다음 탐색 대상은 8번 정점입니다.
stack = [8]
SCC = [[3, 2, 1], [7, 6], [5, 4]]
16.
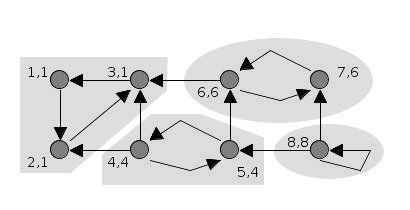
8번 정점은 탐색 대상이 자기 자신 밖에 없고, low 값이 id와 같아 마지막으로 SCC에 추가하는 과정을 거칩니다.
DFS가 완료되었고, 모든 SCC가 확인되었습니다.
stack = []
SCC = [[3, 2, 1], [7, 6], [5, 4], [8]]
https://en.wikipedia.org/wiki/Tarjan's_strongly_connected_components_algorithm
Tarjan's strongly connected components algorithm - Wikipedia
From Wikipedia, the free encyclopedia Graph algorithm Tarjan's strongly connected components algorithm is an algorithm in graph theory for finding the strongly connected components (SCCs) of a directed graph. It runs in linear time, matching the time bound
en.wikipedia.org



