
1. 기본 논리연산
가. 개요
논리 연산이란 주어진 명제에 대하여 참(True) 또는 거짓(False)을 결정하는 연산을 말함.
https://ko.wikipedia.org/wiki/논리_연산
논리 연산 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 논리 연산(logical operation, logical connective) 혹은 불 연산(boolean operation)은 참, 거짓 두 가지 원소(진리값으로 불림)만 존재하는 집합(환으로 불림)에서의 연산이다.
ko.wikipedia.org
나. AND 연산
1) 기본동작
2진수의 입력이 모두 1일 때 1을 출력하고 나머지의 경우에는 0을 출력
2) 진리표
| \(A\) | \(B\) | \(A \times B\) |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
3) 스위치 회로
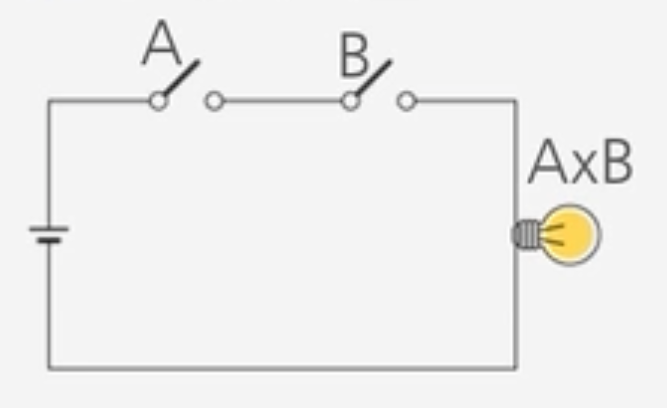
https://ko.wikipedia.org/wiki/논리곱
논리곱 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. AND 논리 게이트 논리곱(conjunction, AND)이란 수리 논리학에서, 주어진 복수 명제 모두가 참인지를 나타내는 논리 연산이다. 두 명제 P, Q에 대한 논리곱을 (P ∧ Q)라
ko.wikipedia.org
다. OR 연산
1) 기본동작
2진수의 입력 중 하나라도 1이면 1을 출력하고, 모든 입력이 0일 때 0을 출력
2) 진리표
| \(A\) | \(B\) | \(A + B\) |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
3) 스위치 회로
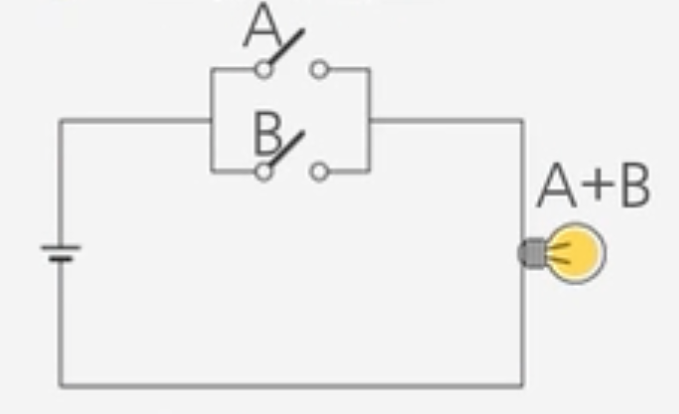
https://ko.wikipedia.org/wiki/논리합
논리합 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 논리합(disjunction, 論理合, OR)이란 수리 논리학에서 주어진 복수 명제에 적어도 1개 이상의 참이 있는지를 나타내는 논리 연산이다. 두 명제 P, Q에 대하여 논리합
ko.wikipedia.org
라. NOT 연산
1) 기본동작
입력에 반대를 출력
2) 진리표
| \(A\) | \(\bar{A}\) |
| 0 | 1 |
| 1 | 0 |
https://ko.wikipedia.org/wiki/부정_(논리학)
부정 (논리학) - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 수리 논리학에서 부정(否定)은 명제의 참과 거짓을 반전하는 논리 연산이다. 명제 P에 대한 부정을 ¬P, P ¯ {\displaystyle {\bar {P}}} , ~p, !P등으로 쓰고, ‘P 가 아니
ko.wikipedia.org
마. XOR(Exclusive-OR) 연산
1) 기본동작
2진수의 입력이 모두 동일할 경우에는 0이고, 나머지의 경우에는 1을 출력
2) 진리표
| \(A\) | \(B\) | \(A \bigoplus B\) |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
https://ko.wikipedia.org/wiki/배타적_논리합
배타적 논리합 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 배타적 논리합(排他的論理合, exclusive or)은 수리 논리학에서 주어진 2개의 명제 가운데 1개만 참일 경우를 판단하는 논리 연산이다. 약칭으로 XOR, EOR, EXOR라고도
ko.wikipedia.org
2. 응용 논리연산
가. 마스크 연산(AND 연산)
1) 기본동작
원하는 비트들을 선택적으로 clear(0)
특정 위치의 비트나 문자를 삭제하는 연산
데이터의 특정 비트들을 0으로 바꾸기 위해서, 원하는 특정 비트위치가 0으로 설정된 Mask와 AND 연산을 수행
2) 예시
데이터 A(10010010)의 상위 4비트를 0으로 clear하시오.
1. 마스크 비트(Mask)를 00001111로 만듦.(상위 4비트를 clear하기 위해)
2. 기존 데이터 A와 마스크 비트를 AND 연산 수행
3. 결과: 00000010
나. 선택적-세트 연산(OR 연산)
1) 기본동작
2진수의 특정 비트를 선택하여 1로 설정
특정 비트 또는 문자를 삽입하거나 결합 시 사용
2) 예시
데이터 A(10010010)의 하위 4비트를 1로 설정하시오.
1. 데이터 B를 00001111로 만듦.(하위 4비트를 1로 설정하기 위해)
2. 데이터 A와 데이터 B를 OR 연산 수행
3. 결과: 10011111
다. 선택적-보수 연산(XOR 연산)
1) 기본동작
2진수의 특정 비트를 1의 보수로 변경시키는 연산
즉, 지정된 비트가 반전됨.
원하는 특정 비트 위치가 1로 세트된 데이터와 XOR 연산
2) 예시
데이터 A(10010010)의 하위 4비트를 반전시켜라.
1. 데이터 B를 00001111로 만듦.(하위 4비트를 반전시키기 위해)
2. 데이터 A와 데이터 B를 XOR 연산 수행
3. 결과: 10011101
라. 삽입 연산(AND, OR 연산)
1) 기본동작
2진 데이터 내의 특정 위치에 새로운 비트 값들을 삽입하는 연산
마스크 연산과 선택적 세트 연산을 순차적으로 수행
삽입할 비트 위치들을 마스크 연산, 새로이 삽입할 비트들과 선택적 세트 연산을 수행
2) 예시
데이터 A(10010010)의 하위 4비트를 1100로 바꿔라.
1. 마스크 비트를 11110000으로 만듦.
2. 데이터 A와 마스크 비트를 AND 연산 수행
3. 결과: 10010000
4. 데이터 B를 00001100으로 만듦.
5. 마스크 연산 결과와 데이터 B를 OR 연산 수행
6. 결과: 10011100
마. 비교 연산(XOR 연산)
1) 기본동작
두 데이터를 비교하는 연산
XOR연산으로 구현
결과가 모두 0이면 같은 경우임.
데이터 A와 B의 내용을 비교하여, 만약 대응되는 비트들의 값이 서로 같으면 0, 서로 다르면 1로 설정
2) 예시
데이터 A(11100001)와 데이터 B(01011001)를 비교해서 값이 같은 자리는 0, 다른 자리는 1로 만들어라.
1. 데이터 A와 데이터 B를 XOR 연산 수행
2. 결과: 10111000
바. 순환 이동 연산(ROTATE 연산)
1) 기본동작
최상위 혹은 최하위에 있는 비트가 반대편 끝에 있는 비트 위치로 이동해서 비트가 회전함.
순환 좌측 이동과 순환 우측 이동이 있음.
사. 산술적 이동 연산(SHIFT 연산)
1) 기본동작
이동 과정에서 부호 비트는 유지하고, 수의 크기를 나타내는 비트들만 이동
산술적 좌측 이동과 산술적 우측 이동이 있음.
2) 특징
좌측으로 한 비트씩 이동 시킬 때마다 2로 곱한 것과 같은 결과가 됨.
좌측으로 n비트 이동시킨 결과 = 원래의 수\( \times 2^{n}\)
우측으로 한 비트 이동 시킬 때마다 2로 나눈 것과 같은 결과가 됨.
우측으로 n비트 이동시킨 결과 = 원래의 수\( \div 2^{n}\)
아. 논리적 이동 연산
1) 기본동작
이동 과정에서 부호 비트를 고려하지 않고 왼쪽 또는 오른쪽으로 한 비트씩 이동
논리적 좌측 이동과 논리적 우측 이동이 있음.



